It is official, as of MAY/2014 I am not working anymore on this.
It was a nice and exciting project that helped me understand a lot of things. But at this point, I prefer not to re-invent the wheel, so I am using open-source and commercial solvers (OpenFOAM, SU2, code saturne, overture, Ansys fluids, and many more). I did not know what I was doing back in the day, and today I do not recall what I was doing. I forgot a lot of things during the years. Maybe from time to time, I will play a little bit with this solver, but it will not be serious.
It was a nice and exciting project that helped me understand a lot of things. But at this point, I prefer not to re-invent the wheel, so I am using open-source and commercial solvers (OpenFOAM, SU2, code saturne, overture, Ansys fluids, and many more). I did not know what I was doing back in the day, and today I do not recall what I was doing. I forgot a lot of things during the years. Maybe from time to time, I will play a little bit with this solver, but it will not be serious.
Finally, after several years of really slow and quiet work, I am almost done with my 2D Euler solver. It is written using clear Fortran 90 (at least that is what I think) and is freely distributed. It is an unstructured 2D Euler solver (finite volume method), which uses Roe's Riemann solver.
I am still tuning it up (as of JAN/2012), and I hope to have it fully optimized someday. I am currently adding some OpenMP instructions, but the code should run fine in parallel using automatic parallelization. I was able to test it on a NEC SX8 vector computer using 32 processors, and the speedup was almost linear, but it was not easy to vectorize.
Just some final words, do not expect too much from this solver. It has been the fruit of my passion for CFD, aerodynamics, and numerical methods, and was coded during my spare time.
General description
2DEUNS is a 2D Euler unstructured finite volume solver. Currently, it only supports unstructured triangular meshes, but plans exist to add quad meshes support, AMR, and moving bodies (sweet). The solver uses Roe's approximate Riemann solver; this formulation is first-order accurate in space; spatial high-order accuracy is obtained using a MUSCL type scheme. The solver is explicit on time, and I may add it is very stable (as long as the CFL is less than one).
The source code is self-explanatory, as long as you know how to program in Fortran 90 (you do not need to be an expert). To run a case, you only need to change a few parameters in the DATA file (case setup) and have the mesh in the right format. To get the mesh in the right format you can read the source code or use the additional meshing tools.
Download the source code
Download the additional meshing tools
In additional meshing tools you will find two programs, domaincreator_triangle and triangle_convert. You can use domaincreator_triangle to read the UIUC airfoil coordinates files (https://m-selig.ae.illinois.edu/ads/coord_database.html) or airfoils coordinates from airfoiltools (http://www.airfoiltools.com/), and then create an input file (*.poly) to be used with Triangle mesher (J.R. Shewchuk).
After generating the mesh using Triangle mesher, you can use the program triangle_convert to convert the output mesh from Triangle into the input mesh format to be used with 2DEUNS. The program triangle_convert, will read the files *.ele and *.node from triangle and create the right mesh format for 2DEUNS. The output of the program is named output.txt, you will need to rename this file to mesh.txt and put it together with the input file DATA into a single directory. Be sure to use the right boundary markers for the boundary conditions (check both programs domaincreator_triangle and triangle_convert). At this point, you are ready to run 2DEUNS. In the directory testcases, you will find a few examples.
On Windows machines, you can compile the source code using digital visual Fortran (it appears that it does not exist anymore), Intel Fortran compiler, or Cygwin. If you are working in a Linux/Unix machine (including MACOS), you can use the makefile distributed with the source code (remember to change the name of the compiler to fit the compiler installed in your system). In general, the compilation is straightforward.
By default, the output files are written in Tecplot and VTK formats. The VTK output can be visualized using Paraview (or any sicientific visualization software that supports VTK). The Tecplot output can also be visualized using Paraview.
For mesh generation, you can use Triangle (J.R. Shewchuk), EasyMesh (B. Niceno), or DistMesh (P.O. Persson). For a description of the required format, take a look at the test cases, 2DEUNS source code, or the source code of the additional meshing tools. Currently, I am working in getting the meshes directly from Gambit or GMSH.
If you have questions of suggestions, please email me. And remember, this solver is very experimental.
2DEUNS in action
-
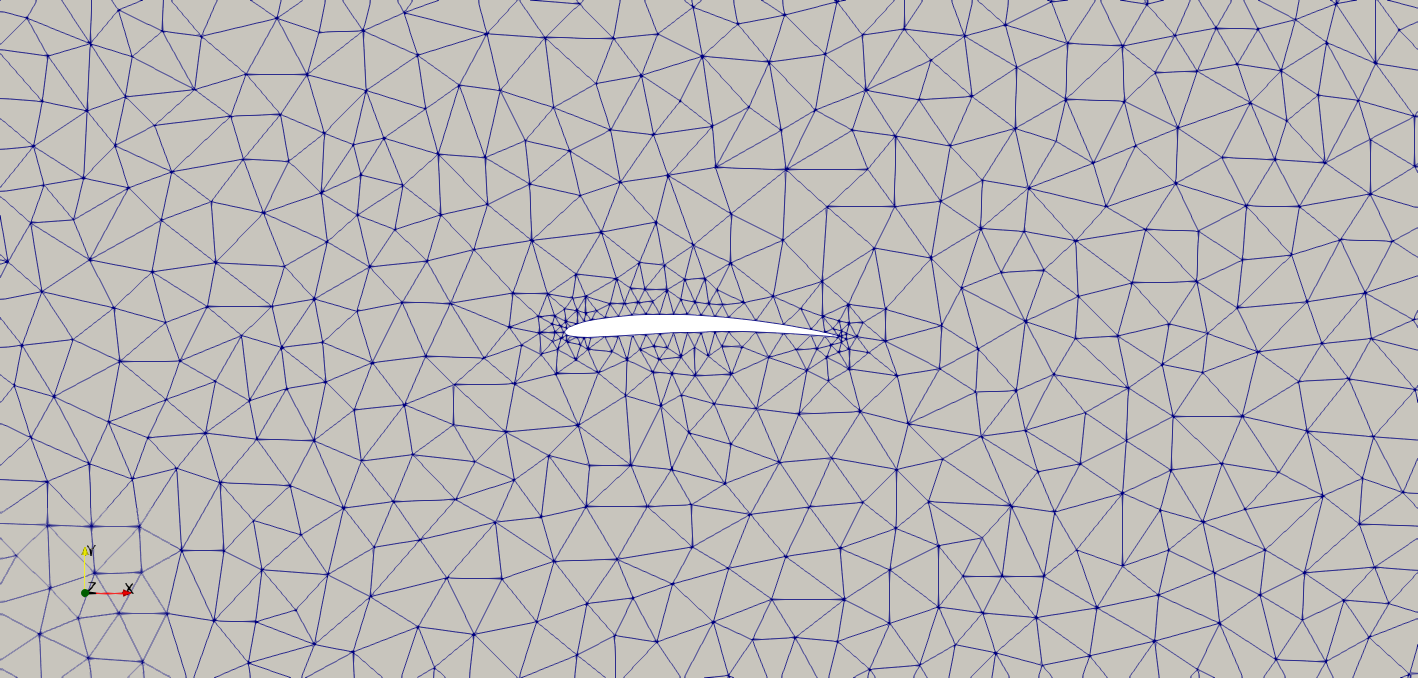
High speed flow around Whitcomb supercritical airfoil. Steady simulation using local-time stepping. The results were obtained for an angle of attack equal to 0 degrees and a Mach number equal to 0.85. Notice that the mesh is extremelly coarse.




-
Low speed flow around a square. Unsteady simulation with a maximum CFL number equal to one. The results were obtained for a Mach number equal to 0.3.



-
High speed flow around an A18 airfoil. Steady simulation using local-time stepping. The results were obtained for an angle of attack equal to 05 degrees and a Mach number equal to 0.7.