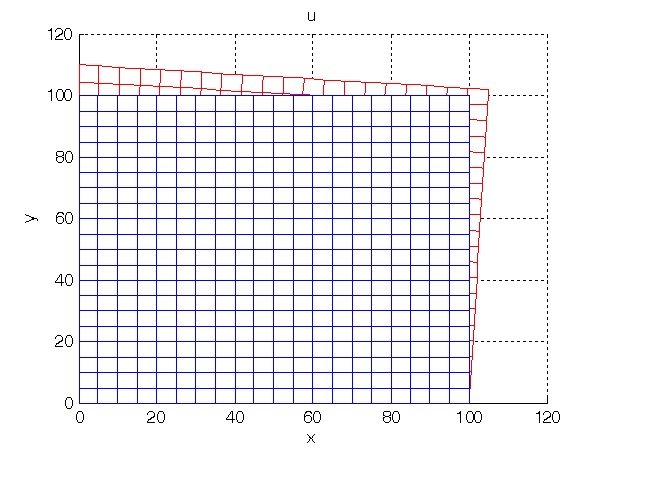
Soluzione numerica in termini di
spostamenti di un problema piano in un dominio rettangolare
(condizioni al contorno cinematiche)
Si consideri un problema elastico in stato piano di tensione nel dominio rettangolare di lati lx=100 e ly=100. Inoltre sia: E = 2.1 105, n = 0.3, bx = by = 0.
Condizioni al contorno:
| y = 0 |
u(x, 0) = 0 |
| x = 0 | u(0, y) = 0 v(0, y) = ay |
| x = lx | u(lx ,y) = bx v(lx, y) = by |
| y = ly | u(x, ly) = b ly/lx
x v(x, ly) = a ly + (c - a) ly/lx x |
a = 0.001, b = 0.0005, c = 0.0002

Figura 1. Spostamento
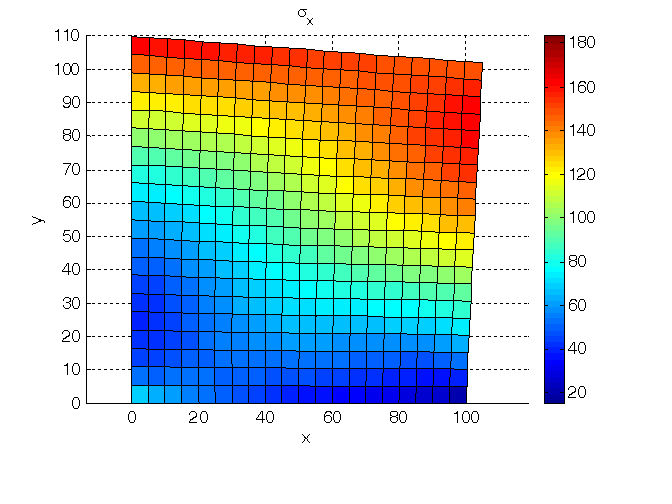
Figura 2. Tensione normale su piani di normale x.
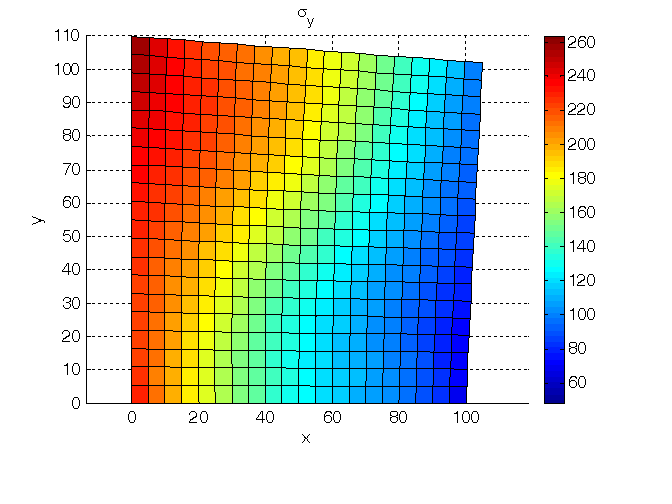
Figura 3. Tensione normale su piani di normale y.
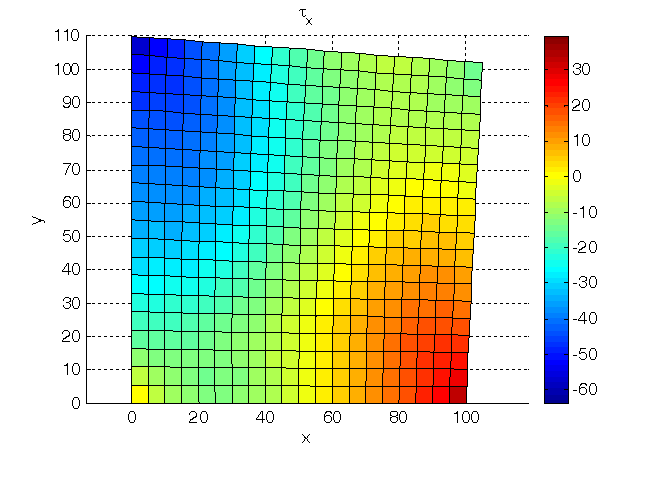
Figura 4. Tensione tangenziale in direzione x su piani di normale y (oppure in direzione y su piani di normale x).
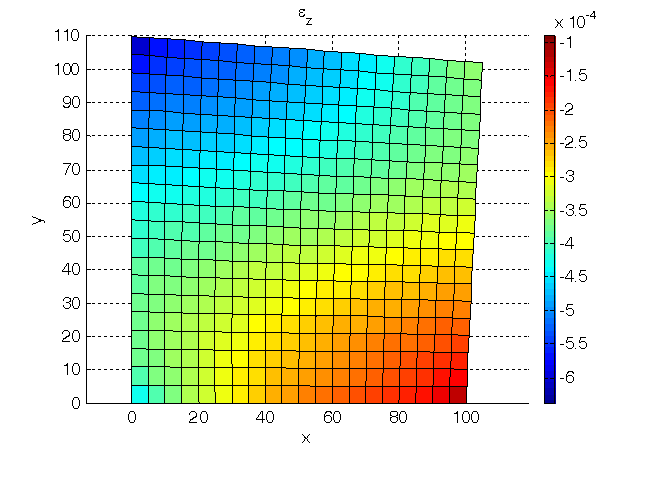
Figura 5. Deformazione longitudinale in direzione z.
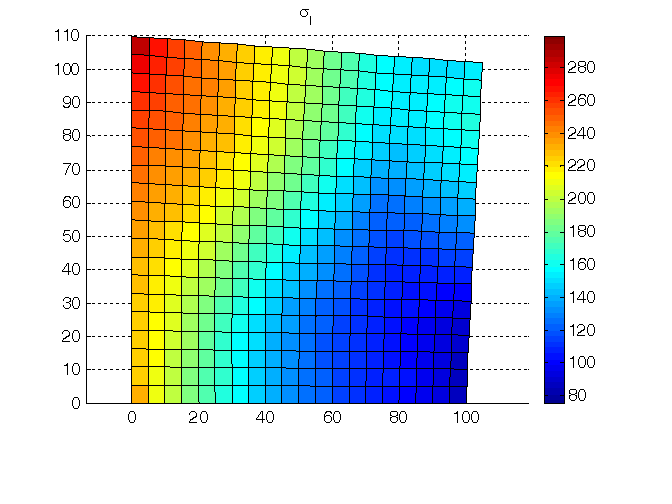
Figura 6. Prima tensione principale.
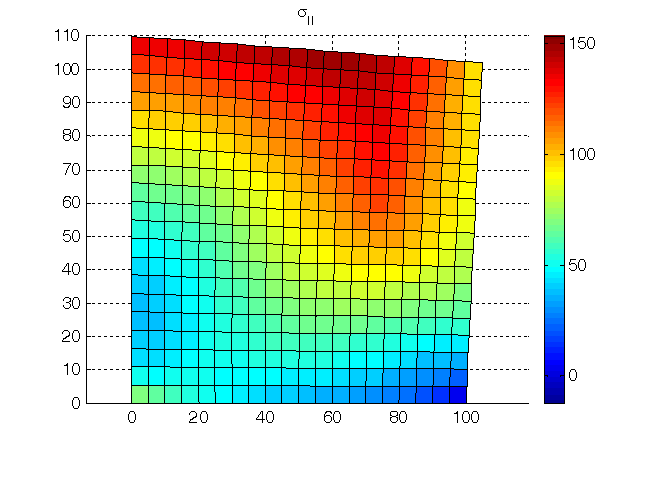
Figura 7. Seconda tensione principale.
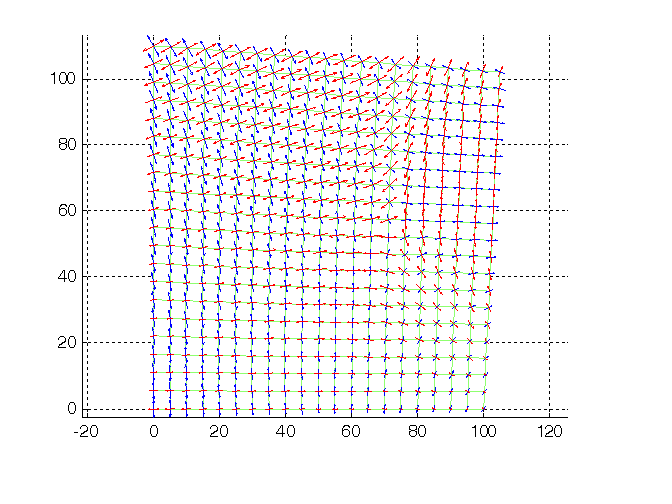
Figura 6. Direzioni principali (prima --, seconda --).
Codice Matlab per soluzione numerica mediante differenze finite.